MiBlog

随机性 序章

2023-10-14

English Version: Stochasticity Prologue

标签: 信号处理 测量与概率 空间随机

基本信息与免责声明

这个博文主要是我记录自己学习信号处理、测量与概率、空间随机性课程时可以通用的知识。如果有时间，里面的一些内容会进一步扩充形成新的博文，所以名字叫做“序章”。但一般情况下，我会尽可能少写点东西，写清楚一点，就留在这篇博文里。

本文可能会大量的掺杂我自己的理解和假设，但是都会标明。我尝试使用轻松日常的语气和阐述方式来写所有的东西。

由于学习过程中或多或少会忽略这些知识的来源到底是哪本书、哪位教授、哪篇博文，精密的记录几乎不可能。我无法为所有的引用做出显式的标记，更不用说部分内容是由GPT编写的，所以敬请理解。

在我编写的过程中，我会时不时更新一下目录。但目前来说，主要就是一些测量与概率的基础知识，以及各种经典分布。

参考资料

  1. STAT 810 Probability Theory I
  2. Measure and Probability - Ulf Fiebig(2019)
  3. Sptial Stochastics I - D.Schuhmacher(2023)
  4. StackExchange
  5. Stochastic process, Keeler
  6. General theory of SP, Uni-ULM
  7. The math founda of prob
  8. Sample path: what is “by fixing w?”
  9. 马尔科夫链以及转移矩阵的简单案例以及python实现
  10. 马尔可夫链算法详解以及Python实现
  11. Chapter 8: Markov Chains

不确定性与随机变量

这是所有问题的基础，也是令人兴奋的动机。手推高斯p.d.f.的爱因斯坦认为不确定性是不存在的，它之所以被研究是因为人类的知识系统和观测手段是存在缺陷的。也就是所谓“上帝不掷骰子”。一些实验也侧面证明了这种观点，例如如果将所有变量严格控制，硬币实验的结果将会非常接近于100%比0%，而非50%对50%。但贝尔实验证明了爱因斯坦的假设“隐变量”是错误的，所以量子力学目前仍然是学术界的大多数选择。

题外话：隐变量证伪的过程可能是有争议的，因为实验的设置可能并非那么坚不可摧，所以请保持怀疑。

我个人会把研究不确定性的动机放在验证不确定性的确定性规则上面。据我有限的知识，我觉得上帝有可能真的不掷骰子。但是问题在于，如果人类的观测有一种天生的限制——例如：我们当然无法观测更高维的事物，在此基础上的任何逻辑都是假设（当然也许我们有方法观测，只是我才疏学浅并不了解这方面的物理研究）；我们也无法真正理解或者思考那些不在我们认知范围内的事物，这可以联系到费曼的那句话“What I cannot create, I do not understand”，也许那些我们从未体验的内容，我们也是无法理解的。所以，如果我们在观测一个并不属于我们理解范围内的对象，很可能我们就无法完整的观测它。

例如一个2x2（二维）的矩阵，他的元素分别为1,2,3,4

$$A = \begin{pmatrix} 1 & 2 \
3 & 4 \end{pmatrix}$$

如果我们从列（一维）的角度看，我们只能看到

$$ A^\prime = \begin{pmatrix} a \
b \end{pmatrix} $$

由于一次只能观测一列，我们无法完整观察这个对象。当我们从一维观测二维对象时，这中间可能会产生一种未知，因为我们不知道具体的规则。当我们观测这个矩阵A时，我们获得的观测理论上可以是任何数字，可能是(3,7) 也就是1+2和3+4；也可能是(1,3)；当然也可能是随机出现的随机数。

为了研究未知和不确定性，我们便需要做统计实验。我们期待用设计好的重复多次的统计实验来观测不确定性。从这里出发，我们正式进入了测量与概率的领域。这时候，我们需要预先确定一些东西的定义，以保证我们逻辑的完备。

TODO

【定义】样本空间 Sample Space：样本空间是实验可能产生的所有结果的集合。通常我们用字母 $\Omega$ 表示它（也有用S和U表示的）。

样本空间的确定实际上是我们对于随机方式的确定。从伯特兰悖论中我们可略窥一二，法国数学家约瑟夫伯特兰(Joseph Bertrand)在1889年提出的一种悖论演示了我们在同样一个实验中，可以通过选择不同的样本空间来对实验的定义进行控制。一个圆中任取一点，我们可以认为…TODO

【定义】样本点 Sample Point：随机试验中的每个可能结果称为样本点, 也被称为实现(realization). 通常用$\omega \in \Omega$表示.

【定义】概率：概率是从样本空间的子集投影到[0,1]之间的函数。

$$ \mathcal P : \mathcal A \to [0,1] $$

[0,1]是约定俗成。

其中$\mathcal A \in P(\Omega)$ ，即A是Omega的幂集的一个子集

概率或者概率测度(probability measures)在测度论和概率论中的定义其实并不简单。他得定义不得不提到Borel σ-代数。定义中的 $\mathcal A$ 就是定义在样本空间上的一种几何结构。

测度论是概率论的基础，他们之间有着非常密切的联系。在测度论中，我们把概率问题考虑为集合的问题。要想使用测度或者概率对集合系进行描述，那么我们必须保证这个集合是一个可测集。可测集就是不论我们对里面的事件做各种逻辑操作、延长伸展，我们仍然会在这个广场上，严格的定义可以让我们充分的愉快的玩耍。而上文所提到的σ-代数(又被称为σ-域)就是这样一个符合要求的集合系。

具体来说，当我们把测量问题展开到整个实数集 $\mathbb R$ 后，我们会遇到一些新的问题。

在测量一两个实线上两点的长度时，我们可以通过一个简单的函数来做到这一点：我们测量一个区间 $I$ 的距离，也就是点a到点b的距离，可以使用函数 $\lambda(I) := |I_b-I_a|$，我们希望可以用这个函数来测量所有实线集上的所有子集。

对于实数线[0,1]，我们需要为里面的每一个子集A都定义一个概率P(A)。但我们应该如何定义这个概率呢？像伯特兰悖论中所述，我们有多种方法“随机”地定义我们的概率，而把这个概率定义为区间 $I$ 的长度是其中一种选择。

这就要求这个测度 $\mu$ 至少满足3个条件：

  1. $\mu(\emptyset) = 0$ 空集的测度为0；
  2. σ-可加性：任意区间整体的测度等于其中所有元素各自测度之和。
  3. $\mu([0,1)) = 1$

那么顺理成章，我们似乎可以定义一个函数λ来作为我们的概率度量 $P(A):=\lambda (A)$ 其中$A \subset [0,1)$。但是，这样定义的概率测度 $P$ 会有一个性质：对于区间 $[0,1]$ 中的每一个单点集 {$x$} ，它的概率都是0。我们可以通过选择公理(axiom of choice)和连续统假设(continuum hypothesis)证明这样的概率测度在 $[0,1]$ 上是不存在的。

听起来有点抽象，但其实不难理解。因为在标准的Lebesgue测度下，任何单点的测度都是0. 因为实线的分割是无限的（芝诺悖论），我们总能通过“一半的一半”找到更细的分割，我们就很难控制我们的整体概率为1.

如果能像上文中提出的，控制单点的测度均为0，使用两点之间的距离作为测度，就是一个更合理的方案。但问题在于，根据上述提到的选择公理和连续统假设，在 $[0,1)$ 上，这样的概率测量是不存在的。所以我们只能在离散的情况下在实数上找到这种概率测度（离散的时候单点集的概率测度不一定是零）。

所以万能的数学家就想到了一个适应性的解决方案：我们不对实线上的所有子集定义测度，只对一个特定的子集类 $A$ 定义测度。这样一个子类包含了绝大多数我们的应用场景，并且在所有的常见集合理论下都是封闭的。这样的结构被称为sigma-algebra，也就是一些子集的集合（幂集），σ-代数的基本定义如下：

  1. $\Omega \in \mathcal A$ 包含全集
  2. $A \in \mathcal A \mathbb Rightarrow A^C \in \mathcal A$ 对补集封闭(包含每个集合的余集)
  3. $A_i \in \mathcal A \text{ for all } i \in \mathbb N \mathbb Rightarrow \bigcup^{\infty}_{i=1} A_i \in \mathcal A$ 对可数无限并集封闭(对于所有正整数集合，他们的无限并集也属于A)

而Borel σ-代数是一个特殊的σ代数，它实在实数轴上的σ代数，被记为 $\mathcal B_\mathbb R$。符合要求的概率测量P应该满足以下条件：

  1. 非负性：对于所有属于Borel σ-代数的集合系A，都有$P(A) ≥ 0$

回到研究不确定性上，当我们有了上述的定义，我们可以在一个基本概率空间 $(\Omega,\mathcal F,\mathbb P)$ 中进行研究。

已完结：离散的概率测度 $P$ 能在 $\mathcal P(\mathbb R)$ 上定义。

未尽之事：索洛维模型(Solovay)模型中，在不可达基数的存在时证明了实数集的所有子集都可测。但是不可达基数无法在标准结合论系统（ZFC）中得到证明。更多信息：维基百科

【定义】随机过程(stochastic process)：随机过程 $\mathbb X = (Xt){t \in T}$ 是 $E$ 中的随机元素(random elements)的集合(collections)

在$\omega \in \Omega$上评估这个随机过程时(也就是固定一个在样本空间内的样本ω作为已知时), 我们可以在整个随机过程上获得一个从时间步骤到状态空间的映射 $\mathbb X(\omega): T \to E$. 也就是说, 我们从样本空间中选取的$\omega$确定后, 我们的随机过程的不确定项剩下了这个样本发生的时间步骤(t), 自然地我们也可以获得过程中每一个随机元素的映射$X_t(\omega)$, 有时也被写成$\mathbb X(w,t)$. 如此, 我们可以将随机过程$\mathbb X$解释为一个在$E^T$空间上的随机元素. 这里的$E^T$是从时间集合T到E的所有可能的映射(轨迹)的集合, 不只是确定了ω的情况, 包含了任意属于Ω的ω, 所有的可能的随机过程都被包括在这个集合中了.

此时的σ-algebra是:

$$\mathcal E ^T := \sigma(\pi_t;t\in T) = \sigma(\bigcup_{t\in T}\pi_t^{-1}(\mathcal E))$$

举个例子, 对于掷骰子这个随机事件, 我们可以设计一个连续投掷2次的统计实验, 所以我们有$T=2$. 我们有$(\Omega,\mathcal F, \mathbb P)$, 其中样本空间为$\Omega = (1,2,3,4,5,6)$, 概率测度$\mathbb P = \frac{1}{6}$.

我们认为的将骰子的六个面分为三类, 分别是上中下, 分别给与三个数字作为标识. 也就是摇到1和2都算1分, 3或4都算2分, 以此类推. 那么, 状态空间$E = (1,2,3)$;

假设我们令样本点$ω=3$, 此时我们获得了一个从 $T\to E$ 的映射 $X(3,t)$, 当 $t=1$ 时, $E=2$; 当 $t=2$ 时, $E=2...$, 可以记作$X_1(3),X_2(3)$. 此时, 我们令$E^T$为$T \to E$的映射(函数)的空间. 也就是在这里存储了所有的可能性$E^T = [(1,1);(1,2);(1,3);(2,1)...)]$, 共有$E^T=9$个元素. 此时的σ-代数就是:

$$\mathcal {E}^T = \sigma(\bigcup_{t\in 3}\pi_t^{-1}(\mathcal E)) = (\emptyset, (1), (2),(3),...,(1,1),...,(3,3))$$

!!! 需要明确一点, 到底抛硬币2次的随机过程的样本空间是(HH,HT,TH,TT)还是(H,T).

在随机过程的上下文中，每个样本 ω 在 Ω 中都对应于一个函数，这个函数给出了时间 T 上每一个点的状态。也就是说，每个 ω 对应于一条从 T 到 E 的路径。因此，Ω 实际上是所有可能路径的集合，而每条路径都是时间对状态的一个函数。

🗿[定义]样本函数(Sample Function): 随机过程的一个单独的输出被称作样本函数, 样本轨迹(sample path), 或者一个实现. 这是相对于随机变量的outcome/样本点的.

🗿【定义】随机元素(random elements), 随机变量, 随机向量, 随机序列：随机元素指从一个可测空间到另一个可测空间的可测映射(measurable map):

$$X: (\Omega, \mathcal{B}) \to (\Omega ^\prime, \mathcal{B}^\prime)$$

有时我们也是用(E, \mathcal E) 或者 在矩阵中(S, \mathcal S)来代表新的(prime)可测空间.

🗿【定义】马尔科夫链(MC): 有一个E不为0的随机过程 $(X_n)_{b \in \mathbb Z_+}$ , 若有一个矩阵 $P = (p_{ij})_{i,j \in E}$ 满足以下条件, 则被称为马尔科夫链:

① 马可夫性质(Markov property):

$$\mathbb{P}(X_{n+1} = j | X_0 = i_0, \dots , X_n = i_n) = \mathbb P(X_{n+1} = j | X_n = i) = p_{ij}$$

② 时间齐次性(time homogeneity):

$$\mathbb P(X_0 = i_0,...,X_{n-1}=i_{n-1}, X_n=i)>0$$

此时, 矩阵$P$被称为随机过程$(X_n)_{b \in \mathbb Z_+}$的转移矩阵(transition matrix), 它一定是随机的(所以也被称为stochastic matrix), 也就是每一行的元素之和为一. $P$ 中的元素描述了从 状态$i$ 转移到 状态$j$ 的概率, 说它随机也就是状态$i$转移到所有的$j$的概率和应该为1. 转移矩阵$P$必须列出状态空间所有可能的状态[11]

举个例子, 假设有三个状态 A、B 和 C。如果从状态 A 转移到状态 A 的概率是0.2，转移到状态 B 的概率是0.3，转移到状态 C 的概率是0.5，那么这三个概率之和就是1。这意味着，当你当前处于状态 A 时，你在下一时刻将100%的概率转移到A、B、C中的某一个状态。

直观得来看, ①马尔可夫性质就是假设上一个状态包含了从一开始$X_0$到上一个状态$X_{t-1}$的所有信息, 在这个过程中没有任何损耗. 所以我们就可以心安理得地只用上一个时间步 $X_{t-1}$ 的状态来预测当前时间步的状态$X_t$.

主要思想是不管初始状态是什么，只要状态转移矩阵不发生变化, 最终状态始终会收敛到一个固定值, 这种无记忆性叫马尔科夫属性。这(Markov assumption)是数据融合应用中的著名的假设之一, 被大量运用在自然语言处理, 自动驾驶等领域. 它有效的简化了众多运算, 并把统计结论保持在事实上. 下图中你可以看出, 拥有马尔可夫性质的时序数据(或者说随机变量)可以去除大量不必要的相互关系.

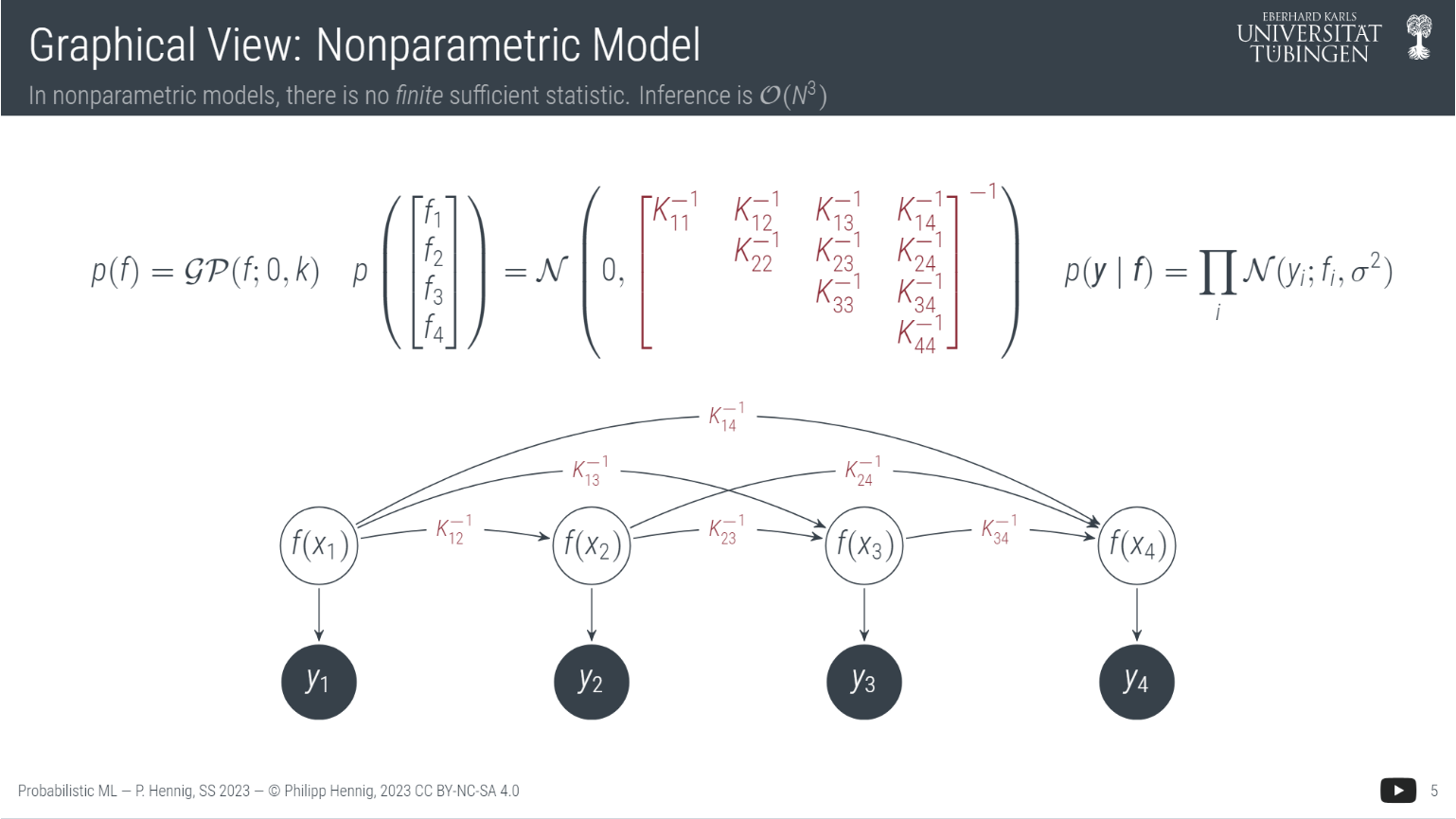
before markov

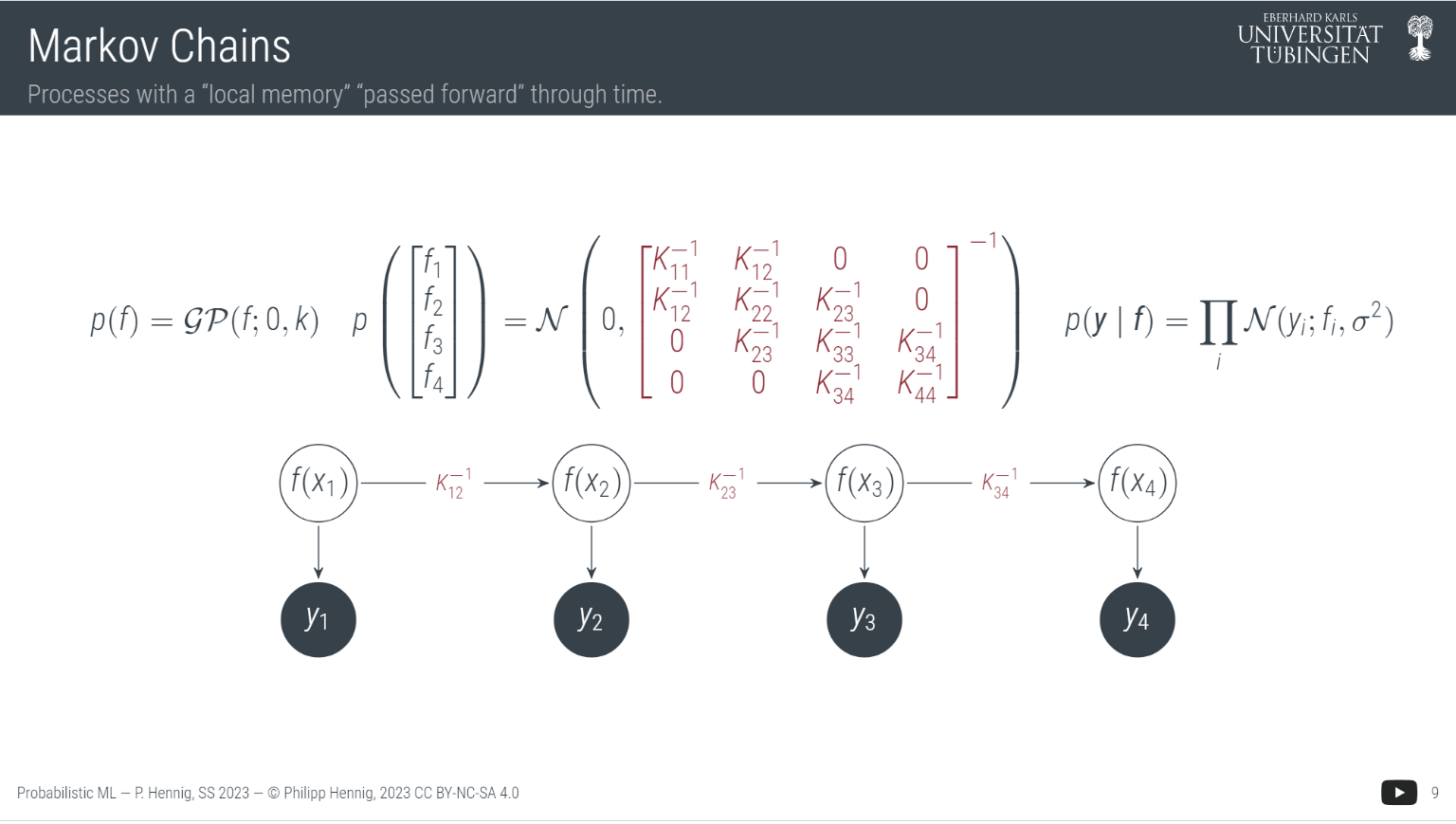
after markov

[定义] 马尔可夫链的初始/起始分布(starting/initial distribution): 向量 $v=(v_i)_{i\in E}$, 其中 $v_i = \mathbb P(X_0 = i)$, 它必须是一个概率向量, 也就是元素之和为1, 这与$X_0$的分布对应.

[引理 1.1] 如果$X_t是\mathcal F - \mathcal E - measurable$

【定义】随机过程的$\mathbb X$分布$\mu$是在可测空间$(E^T, \mathcal E^T)$上的测度.

$$\mu (A) = \mathbb P \mathbb X^{-1}(A)=\mathbb P(\mathbb X \in A) \text{ for every } A \in \mathcal E^T$$

随机过程的分布是一个为轨迹的可测集上的轨迹(paths)分配概率的东西, 描述了随机过程$\mathbb X$沿其中一条特定轨迹演变的可能性.

由上述关于马尔科夫链的定义可以得出, 我们可以获得一定构建出马链的方式：

只要有其初始分布: 一个概率向量$v=(v_i)_{i \in E}$. 以及转移矩阵transition matrix: 一个随机矩阵$P = (p_{ij})_{i,j \in E}$. 就一定可以构建一个马尔科夫链(的随机过程). 这由 Daniell’s Theorem保证. 此外, 随机过程的分布是唯一且确定的(uniquely determined), 这是由随机过程唯一性定理所保证的. 通常我们用M(v,P) 来表示分布, 如果初始分布不重要, 书写时可以省略.

我们可以通过下面的结论来计算与马尔可夫链相关的概率.

🎆[结论1.2.1] 马尔可夫链(MC)的随机过程中, 已知初始状态v0, 可以得到从0到n的轨迹的概率. 可以通过从初始状态v0一直连续乘以相应的状态转移概率(出自转移矩阵)算出: $$\mathbb{P}(X_0=i_0,...,X_n=i_n)=v \cdot p_{i_0,i_1} ... p_{i_{n-1},i_n}$$ 通过这个结论, 我们可以在给定初始状态的条件下, 使用转移矩阵来确定系统在未来某一时刻的状态分布. 该结论可以通过归纳法证明, 在$n=n+1$时, 也成立. 由联合分布和条件分布的定义公式, 以及之前提到的马尔科夫链的定义, 有: $$ \mathbb P(X_0 = i_0, ...,X_{n+1} = i_{n+1}) = v \cdot p_{i_0i_1}...p_{i_ni_{n+1}}$$ 🎆[结论1.2.2] 马尔可夫链(MC)的随机过程中, 已知从0到n都在集合A上, 以及中间状态$Xn=i$, 可以得到从n到n+m(m步以后)的这段特定轨迹的概率. 通过从$p{(i=X_n)}$一直连续乘以相应的状态转移概率(出自转移矩阵)算出: $$P(X_{n+1} = j_1, \ldots, X_{n+m} = j_m | (X_0, \ldots, X_{n-1}) \in A, X_n = i) = p_{ij_1} \cdot p_{j_1j_2} \cdot \ldots \cdot p_{j_{m-1}j_m}$$ 因此我们有: $$P(X_{n+m} = j | (X_0, \ldots, X_{n-1}) \in A, X_n = i) = (P^m)_{ij}$$ 令$p^{(m)}_{ij} := (P^m)_{ij}$, 指从状态$i$经过$m$步到状态$j$的概率. 当$m=0$时, 我们定义其为Kronecker$\delta_{ij}$函数, 当$i=j$时为$1$, 其余为$0$(也就是一个单位矩阵).

🎆[结论1.2.3] 令$\tilde{v_n}=(\tilde{v}_{ni})_{i\in E}:=\mathcal L(X_n)$, 意思是定义了一个在$n$时刻的时刻分布, $\tilde{v}_{ni}$是这个随机过程(链)在此时在状态$i$的概率. 如果我们令$\tilde v_0=v$, 有: $$\tilde{v}^\text{T}_n = v^\text{T}P^n$$ 这个公式的意思是令原始分布乘以转换矩阵的n次幂, 这样就可以得到转移n次后的分布. $P^n$是经过$n$步后的转移矩阵.这个结论可以通过全概率定理将$\mathbb P(X_n=j)$中的所有$X_0=i, i \in E$可能性加起来, 就得到了这个公式. 例如: $$ 初始分布~v = \begin{bmatrix} 0.5 & 0.5 \end{bmatrix}~~转移矩阵~P = \begin{bmatrix} 0.2 & 0.8 \\ 0.4 & 0.6 \end{bmatrix}~~转移矩阵的平方~P^2 = \begin{bmatrix} 0.36 & 0.64 \\ 0.32 & 0.68 \end{bmatrix} $$ $$ v_n = v P^2 = \begin{bmatrix} 0.5 & 0.5 \end{bmatrix} \times \begin{bmatrix} 0.36 & 0.64 \\ 0.32 & 0.68 \end{bmatrix} = \begin{bmatrix} 0.34 & 0.66 \end{bmatrix} $$ 这里的$(P^2)_{11}=0.36$表示从状态$1$经过$2$步转移到状态$1$的概率, 推而广之可以理解之前$(P^m)_{ij}$是指从状态$i$经过$m$次转换到达状态$j$的概率分布.

题外话: 对称随机游走 Symmetric random walk

对称的随机游走是一个马氏链. 它的状态空间$E=\mathbb Z^d$, 初始分布为$v=\delta_0$.

当随机游走是“对称的”时，这意味着在每一步中，移动的概率分布是均匀的。例如，在一维的对称随机游走中，每次移动向左或向右的概率是相等的。这种性质确保了游走过程在统计意义上是无偏的，即没有倾向于向任何方向移动。

对称性给随机游走带来了几个重要的数学特性，例如：

中心极限定理 CLT

中心极限定理（Central Limit Theorem）是概率论中的一个基本定理，它描述了在一定条件下，独立随机变量之和趋向于正态分布，不管这些随机变量本身是否呈正态分布，只要它们满足一定的条件即可。

这个定理在对称随机游走的背景下具有特别的意义。考虑一个简单的一维对称随机游走，每一步都有相等的机会向左或向右移动相同的距离。如果你记录下每一步之后的位置，并多次重复这个过程，那么随着步数的增加，这些位置的分布将趋向于正态分布。这是因为每一步的位置可以被视为一个独立的随机变量，而随机游走的总位移就是这些随机变量的和。

中心极限定理的一些关键点包括：

在随机游走的情况下，中心极限定理说明了为什么在很多步之后，尽管每一步都是随机的，但其总位移的分布却呈现出一定的规律性（即正态分布）。这个现象在物理学的许多领域中都非常重要，比如在描述粒子由于随机碰撞而造成的扩散过程（布朗运动）时。在金融学中，中心极限定理用于解释资产价格变动的分布。在生物学中，它可以解释基因频率的随机波动。

中心极限定理是统计学的基石之一，几乎所有统计推断方法都在某种程度上依赖于它。它使得人们能够对大量观测数据进行合理的统计分析，即使对于那些本身不是正态分布的数据。

要理解中心极限定理, 就要从傅里叶变换对开始.

高斯分布 <- 随机游走 <- 中心极限 <- 特征函数 <- 傅里叶变换 <- 复指数函数 <- 复数 <- 指数函数

与随机游走并列的知识点有: - 利维飞行（Lévy flight）：在这种随机游走中，步长服从一个重尾分布，比如利维分布。利维飞行与更广泛的稳定分布有关，这些分布不一定具有有限的方差或甚至是有限的均值。 - 分数布朗运动（Fractional Brownian motion）：这是一个具有长记忆性质的随机游走，它的增量具有相依性，这与标准布朗运动（即正态分布的随机游走）不同。 - 次线性扩散过程：在某些物理系统中，观察到的是比正态扩散更慢的过程，这可能是由于某种形式的阻碍或陷阱导致的。

强马尔可夫性质 strong Markov property

它允许在随机时间N条件下替换确定时间n，在某些情况下，这可以简化分析和计算。

一个例子是：

import numpy as np

# 设置初始资金和赌注次数
initial_capital = 50
wager_amount = 1
total_wagers = 1000

# 赌徒的目标资金，达到即停止
target_capital = 60

def gamble(capital, wagers, wager_amount, target_capital):
    # 记录每次赌博后的资金
    capital_trajectory = [capital]
    
    # 进行赌博模拟
    for wager in range(wagers):
        if capital == 0 or capital >= target_capital:
            # 赌徒破产或达到目标资金，停止模拟
            break
        if np.random.rand() <= 0.5:
            capital += wager_amount  # 赢了
        else:
            capital -= wager_amount  # 输了
        capital_trajectory.append(capital)
    
    # 返回资金历史
    return capital_trajectory

# 模拟一次赌博过程
capital_history = gamble(initial_capital, total_wagers, wager_amount, target_capital)

# 查找第一次达到目标资金的时刻
try:
    stopping_time = next(i for i, capital in enumerate(capital_history) if capital >= target_capital)
except StopIteration:
    stopping_time = None

# 打印结果
stopping_time, capital_history[:stopping_time+1] if stopping_time is not None else "目标未达到"

我们获得的结果是

(28,
 [50,
  51,
  52,
  51,
  52,
  53,
  52,
  51,
  50,
  49,
  48,
  49,
  48,
  49,
  50,
  51,
  52,
  53,
  52,
  53,
  54,
  53,
  54,
  55,
  56,
  57,
  58,
  59,
  60])

在我们的模拟中，赌徒开始时有50元的初始资金，目标是增加到60元。每一轮赌注，赌徒有50%的几率赢得1元，也有50%的几率输掉1元。在这次模拟中，赌徒在第28次赌注时第一次达到了60元的目标。

模拟的资金历史显示了赌徒的资金在每次赌注后如何变化，直到达到目标或者资金耗尽。在这个特定的模拟中，赌徒在第28次赌注时达到了目标资金，此时我们停止模拟。根据强马尔可夫性质，即使赌徒在这个随机的停止时刻停下来，他之后的赌注结果也只会依赖于当前的资金状态（60元），而与之前的赌注历史无关。

因此，如果赌徒继续赌博，无论之前发生了什么，从第85次赌注开始的每一次赌注的胜率仍然是50%。这就是强马尔可夫性质的一个例证：未来的状态只依赖于当前状态，即使当前状态是在一个随机时间点决定的。​

也就是从t=28 推广到 t=“达到60时”. 也就是从确定的时间推广到不确定的随机时间, 又被称为停止时刻(stopping time).

随机研究中的假设

  1. 独立同分布(i.i.d.)
    • 独立同分布(independent identical distribution)是对于统计实验的经典假设. 它假定了我们的实验和研究的对象是”完美的”, 每次实验不会互相影响, 而且所有实验都遵循同样的概率分布, 这允许我们合法的踏入研究随机事件的大门.